Paint production¶

The problem description in this section is taken from Section 7.5 Paint production of the book Applications of optimization with Xpress-MP. As a part of its weekly production a paint company produces five batches of paints, always the same, for some big clients who have a stable demand. Every paint batch is produced in a single production process, all in the same blender that needs to be cleaned between every two batches. The durations of blending paint batches 1 to 5 are respectively 40, 35, 45, 32, and 50 minutes. The cleaning times depend on the colors and the paint types. For example, a long cleaning period is required if an oil-based paint is produced after a water-based paint, or to produce white paint after a dark color. The times are given in minutes in the following table:

CLEAN(i,j)	1	2	3	4	5
1	0	11	7	13	11
2	5	0	13	15	15
3	13	15	0	23	11
4	9	13	5	0	3
5	3	7	7	7	0

Since the company also has other activities, it wishes to deal with this weekly production in the shortest possible time (blending and cleaning). Which is the corresponding order of paint batches? The order will be applied every week, so the cleaning time between the last batch of one week and the first of the following week needs to be counted for the total duration of cleaning.

Formulation of model 1¶

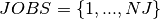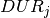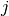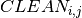As for the problem in section 11.3 we are going to present two alternative model formulations. The first one is closer to the Mathematical Programming formulation in Applications of optimization with Xpress-MP, the second uses a two-dimensional element constraint. Let $JOBS = \{1, ..., NJ\}$ be the set of batches to produce, $DUR_j$ the processing time for batch $j$ , and $CLEAN_{i,j}$ the cleaning time between the consecutive batches 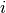$i$ and $j$ . 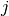We introduce decision variables 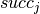$succ_j$ taking their values in 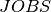$JOBS$ , to indicate the successor of every job, and variables 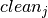$clean_j$ for the duration of the cleaning after every job. The cleaning time after every job is obtained by indexing 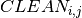$CLEAN_{i,j}$ with the value of 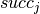$succ_j$ . We thus have the following problem formulation:

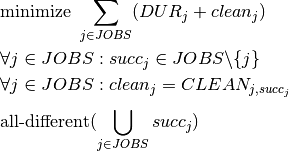
$&\text{minimize } \sum_{j \in JOBS}(DUR_j + clean_j)\\ &\forall j \in JOBS : succ_j \in {JOBS} \backslash \{j\}\\ &\forall j \in JOBS : clean_j = CLEAN_{j,succ_j}\\ &\text{all-different}(\bigcup\limits_{j \in JOBS}^{} succ_j)\\$

The objective function sums up the processing and cleaning times of all batches. The last (all-different) constraint guarantees that every batch occurs exactly once in the production sequence.

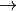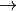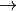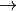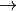Unfortunately, this model does not guarantee that the solution forms a single cycle. Solving it indeed results in a total duration of 239 with an invalid solution that contains two sub-cycles 1 $\rightarrow$ 3 $\rightarrow$ 2 $\rightarrow$ 1 and 4 $\rightarrow$ 5 $\rightarrow$ 4. A first possibility is to add a disjunction excluding this solution to our model and re-solve it iteratively until we reach a solution without sub-cycles.

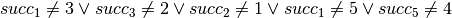
$&succ_1 \ne 3 \vee succ_3 \ne 2 \vee succ_2 \ne 1 \vee succ_1 \ne 5 \vee succ_5 \ne 4\\$

However, this procedure is likely to become impractical with larger data sets since it may potentially introduce an extremely large number of disjunctions. We therefore choose a different, a-priori formulation of the sub-cycle elimination constraints with a variable 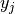$y_j$ per batch and 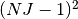$(NJ-1)^2$ implication constraints.

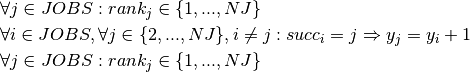
$&\forall j \in JOBS : rank_j \in \{1, ..., NJ\}\\ &\forall i \in JOBS, \forall j \in \{2, ..., NJ\}, i \ne j : succ_i = j \Rightarrow y_j = y_i + 1\\ &\forall j \in JOBS : rank_j \in \{1, ..., NJ\}\\$

The variables 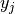$y_j$ correspond to the position of job 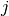$j$ in the production cycle. With these constraints, job 1 always takes the first position.

Implementation of model 1¶

The implementation of the model formulated in the previous section is quite straightforward. The sub-cycle elimination constraints are implemented as logic relations with implies (a stronger formulation of these constraints is obtained by replacing the implications by equivalences, using KEquiv).

// Number of paint batches (=jobs)
int NJ = 5;
// Durations of jobs
int DUR[]  = {40, 35, 45, 32, 50};

// Cleaning times between jobs
int CLEAN[5][5] = {
    {  0, 11,  7, 13, 11 },
    {  5,  0, 13, 15, 15 },
    { 13, 15,  0, 23, 11 },
    {  9, 13,  5,  0,  3 },
    {  3,  7,  7,  7,  0 } };


// Cleaning times after a batch
KIntArray CB;
// Successor of a batch
KIntVarArray succ;
// Cleaning time after batches
KIntVarArray clean;
// Variables for excluding subtours
KIntVarArray y;
// Objective variable
KIntVar * cycleTime;

// Creation of the problem in this session
KProblem problem(session,"B-5 Paint production");

// variables creation
char name[80];
int j,i;
for (j=0;j<NJ;j++) {
    sprintf(name,"succ(%i)",j);
    succ += (* new KIntVar( problem,name,0,NJ-1) );
    succ[j].remVal(j);
    sprintf(name,"y(%i)",j);
    y += (* new KIntVar( problem,name,0,NJ-1) );
}

// initialization of CB array
for (j=0;j<NJ;j++) {
    CB += 0;
}
// Cleaning time after every batch
for (j=0;j<NJ;j++) {
    sprintf(name,"clean(%i)",j);
    clean += (* new KIntVar( problem,name,0,1000) );
    for (i=0;i<NJ;i++) {
        CB[i] = CLEAN[j][i];
    }
    KEltTerm kelt(CB,succ[j]);
    problem.post(new KElement(kelt,clean[j],"element"));
}

// objective variable creation
cycleTime = new KIntVar(problem,"cycleTime",0,1000);
// Objective: minimize the duration of a production cycle
KLinTerm cycleTerm;
for (j=0;j<NJ;j++) {
    cycleTerm = cycleTerm + clean[j] + DUR[j];
}
problem.post(cycleTerm == *cycleTime);

// One successor and one predecessor per batch
problem.post(new KAllDifferent("alldiff",succ));

// Exclude subtours
for (i=0;i<NJ;i++) {
    for (j=1;j<NJ;j++) {
        if (i!=j) {
            problem.post(new KGuard( succ[i] == j , y[j] == y[i] + 1  );                }
    }
}
// propagating problem
if (problem.propagate()) {
    printf("Problem is infeasible\n");
    exit(1);
}

// Solve the problem
// creation of the solver
KSolver solver(problem);

// setting objective and sense of optimization
problem.setSense(KProblem::Minimize);
problem.setObjective(*cycleTime);

int result = solver.optimize();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();


// Solution printing
printf("Minimum cycle time: %i\n", sol->getValue(*cycleTime));
printf("Sequence of batches:\nBatch Duration Cleaning\n");
int first=0;
do {
    printf("%i\t%i\t%i\n", first, DUR[first],sol->getValue(clean[first]));
    first = sol->getValue(succ[first]);
} while (first!=0);

from kalis import *

### Data
# Number of paint batches (=jobs)
nb_jobs = 5
# Durations of jobs
jobs_durations  = [40, 35, 45, 32, 50]

# Cleaning times between jobs
jobs_cleaning_times = [[0, 11, 7, 13, 11],
            [5, 0, 13, 15, 15],
            [13, 15, 0, 23, 11],
            [9, 13, 5, 0, 3],
            [3, 7, 7, 7, 0]]
max_cleaning_time = max(max(jobs_cleaning_times[j]) for j in range(nb_jobs))

### Creation of the problem
# Creation of the Kalis session
session = KSession()

# Creation of the optimization problem
problem = KProblem(session, "B-5 Paint production")

### Variables creation
# Successor of a batch
batch_successor = KIntVarArray()
for j in range(nb_jobs):
    batch_successor += KIntVar(problem, "succ(%d)" % j, 0, nb_jobs - 1)
    batch_successor[j].remVal(j)


# Cleaning times after a batch
batch_cleaning_time = KIntVarArray()
for j in range(nb_jobs):
    batch_cleaning_time += KIntVar(problem, "clean(%d)" % j, 0, max_cleaning_time)

# Variables for excluding subtours
job_position_in_cycle = KIntVarArray() # i.e. y_j variables
for j in range(nb_jobs):
    job_position_in_cycle += KIntVar(problem, "y(%d)" % j, 0, nb_jobs - 1)

### Constraints creation
# Cleaning time after every batch:
# i.e. "batch_cleaning_time[j] == jobs_cleaning_times[batch_succesor[j]]"
for j in range(nb_jobs):
    K_cleaning_time = KIntArray() # convert Python list to KIntArray
    for i in range(nb_jobs):
        res = K_cleaning_time.add(jobs_cleaning_times[j][i])
    kelt = KEltTerm(K_cleaning_time, batch_successor[j])
    problem.post(kelt == batch_cleaning_time[j])

# One successor and on predecessor per batch
problem.post(KAllDifferent("alldiff", batch_successor))

# Exclude subtours
for i in range(nb_jobs):
    for j in range(1, nb_jobs):
        if i != j:
            problem.post( KGuard(batch_successor[i] == j,
                        job_position_in_cycle[j] == (job_position_in_cycle[i] + 1)))

# Set objective
cycle_time = KIntVar(problem, "cycle_time", 0, 1000)
batch_cleaning_times_sum = 0
for j in range(nb_jobs):
    batch_cleaning_times_sum += batch_cleaning_time[j]
problem.post(cycle_time == (batch_cleaning_times_sum + sum(jobs_durations)))

# First propagation to check inconsistency
if problem.propagate():
    print("Problem is infeasible")
    sys.exit(1)

### Solve the problem
# Set the solver
solver = KSolver(problem)

# Setting objective and sense of optimization
problem.setSense(KProblem.Minimize)
problem.setObjective(cycle_time)

# Run optimization
result = solver.optimize()
# Solution printing
if result:
    solution = problem.getSolution()
    solution.printResume()
    print("Minimum cycle time: %d" % solution.getValue(cycle_time))
    print("Sequence of batches:")
    print("Batch Duration Cleaning")
    j = solution.getValue(batch_successor[0])
    while j != 0:
        print("%d\t%d\t%d" % (j, jobs_durations[j],
                 solution.getValue(batch_cleaning_time[j])))
        j = solution.getValue(batch_successor[j])

// Number of paint batches (=jobs)
int NJ = 5;
// Durations of jobs
int[] DUR = {40, 35, 45 ,32 ,50};

// Cleaning times between jobs
int[][] CLEAN = {
        {  0, 11,  7, 13, 11 },
        {  5,  0, 13, 15, 15 },
        { 13, 15,  0, 23, 11 },
        {  9, 13,  5,  0,  3 },
        {  3,  7,  7,  7,  0 } };

// Cleaning times after a batch
KIntArray CB = new KIntArray();
// Successor of a batch
KIntVarArray succ = new KIntVarArray();
// Cleaning time after batches
KIntVarArray clean = new KIntVarArray();
// Variables for excluding subtours
KIntVarArray y = new KIntVarArray();
// Objective variable
KIntVar cycleTime = new KIntVar();

// Creation of the problem in this session
KProblem problem = new KProblem(session,"B-5 Paint production");

// variables creation
int j,i;
for (j=0;j<NJ;j++)
{
    succ.add(new KIntVar(problem,"succ(" + j + ")",0,NJ-1));
    succ.getElt(j).remVal(j);
    y.add(new KIntVar(problem,"y(" + j + ")",0,NJ-1));
}

// Cleaning time after every batch
for (j=0;j<NJ;j++)
{
    clean.add(new KIntVar(problem,"clean(" + j + ")",0,1000) );
    for (i=0;i<NJ;i++)
    {
        CB.add(CLEAN[j][i]);
    }
    KEltTerm kelt = new KEltTerm(CB,succ.getElt(j));
    problem.post(new KElement(kelt,clean.getElt(j),"element"));
}

// objective variable creation
cycleTime = new KIntVar(problem,"cycleTime",0,1000);
// Objective: minimize the duration of a production cycle
KLinTerm cycleTerm = new KLinTerm();
int sumOfDUR = 0;
for (j=0;j<NJ;j++)
{
    cycleTerm.add(clean.getElt(j),1);
    sumOfDUR += DUR[j];
}

KNumVarArray intVarArrayToSet = cycleTerm.getLvars();
KDoubleArray coeffsToSet = cycleTerm.getCoeffs();
intVarArrayToSet.add(cycleTime);
coeffsToSet.add(-1);
problem.post(new KNumLinComb("",coeffsToSet,intVarArrayToSet,-sumOfDUR,KNumLinComb.LinCombOperator.Equal));

// One successor and one predecessor per batch
problem.post(new KAllDifferent("alldiff",succ));

// Exclude subtours
for (i=0;i<NJ;i++)
{
    for (j=1;j<NJ;j++)
    {
        if (i!=j)
        {
            problem.post(new KGuard( new KEqualXc(succ.getElt(i),j) , new KGreaterOrEqualXyc(y.getElt(j),y.getElt(i), 1)));
        }
    }
}
// propagating problem
if (problem.propagate())
{
    System.out.println("Problem is infeasible");
    exit(1);
}

// Solve the problem
// creation of the solver
KSolver solver = new KSolver(problem);

// setting objective and sense of optimization
problem.setSense(KProblem.Sense.Minimize);
problem.setObjective(cycleTime);

int result = solver.optimize();
// solution printing
KSolution sol = problem.getSolution();
// print solution resume
sol.printResume();


// Solution printing
System.out.println("Minimum cycle time: " + sol.getValue(cycleTime));
System.out.println("Sequence of batches:");
System.out.println("Batch Duration Cleaning:");
int first=0;
do {
    System.out.print(first + "\t" + DUR[first] + "\t" + sol.getValue(clean.getElt(first)) + "\n");
    first = sol.getValue(succ.getElt(first));
} while (first!=0);

Formulation of model 2¶

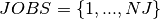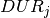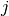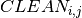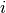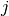We may choose to implement the paint production problem using rank variables similarly to the sequencing model in section 11.3. As before, let $JOBS = \{1, ..., NJ\}$ be the set of batches to produce, $DUR_j$ the processing time for batch $j$ , and $CLEAN_{i,j}$ the cleaning time between the consecutive batches $i$ and $j$ . We introduce decision variables 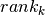$rank_k$ taking their values in 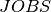$JOBS$ , for the number of the job in position 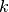$k$ . 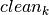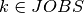Variables $clean_k$ with $k \in JOBS$ now denote the duration of the 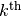$k^{\text{th}}$ cleaning time. This duration is obtained by indexing 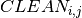$CLEAN_{i,j}$ with the values of two consecutive 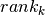$rank_k$ variables. We thus have the following problem formulation.

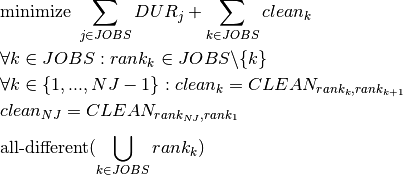
$&\text{minimize } \sum_{j \in JOBS}DUR_j + \sum_{k \in JOBS}clean_k\\ &\forall k \in JOBS : rank_k \in {JOBS} \backslash \{k\}\\ &\forall k \in \{1, ..., NJ-1\} : clean_k = CLEAN_{rank_k,rank_{k+1}}\\ & clean_{NJ} = CLEAN_{rank_{NJ},rank_{1}}\\ &\text{all-different}(\bigcup\limits_{k \in JOBS}^{} rank_k)\\$

As in model 1, the objective function sums up the processing and cleaning times of all batches. Although not strictly necessary from the mathematical point of view, we use different sum indices for durations and cleaning times to show the difference between summing over jobs or job positions. We now have an all-different constraint over the rank variables to guarantee that every batch occurs exactly once in the production sequence.

Implementation of model 2¶

The implementation of the second model uses the 2-dimensional version of the KElement constraint in Artelys Kalis.

// Number of paint batches (=jobs)
int NJ = 5;
// Durations of jobs
int DUR[]  = {40, 35, 45 ,32 ,50};

// Cleaning times between jobs
KIntMatrix CLEAN(5,5,0,"CLEAN");

CLEAN[0][0] = 0;CLEAN[1][0] = 11;CLEAN[2][0] = 7;CLEAN[3][0] = 13;CLEAN[4][0] = 11;
CLEAN[0][1] = 5;CLEAN[1][1] = 0;CLEAN[2][1] = 13;CLEAN[3][1] = 15;CLEAN[4][1] = 15;
CLEAN[0][2] = 13;CLEAN[1][2] = 15;CLEAN[2][2] = 0;CLEAN[3][2] = 23;CLEAN[4][2] = 11;
CLEAN[0][3] = 9;CLEAN[1][3] = 13;CLEAN[2][3] = 5;CLEAN[3][3] = 0;CLEAN[4][3] = 3;
CLEAN[0][4] = 3;CLEAN[1][4] = 7;CLEAN[2][4] = 7;CLEAN[3][4] = 7;CLEAN[4][4] = 0;

// Successor of a batch
KIntVarArray rank;
// Cleaning time after batches
KIntVarArray clean;
// Objective variable
KIntVar * cycleTime;

// Creation of the problem in this session
KProblem problem(session,"B-5 Paint production");

// variables creation
char name[80];
int k,j,i;
for (j=0;j<NJ;j++) {
    sprintf(name,"rank(%i)",j);
    rank += (* new KIntVar( problem,name,0,NJ-1) );
    sprintf(name,"clean(%i)",j);
    clean += (* new KIntVar( problem,name,0,1000) );
}

// Cleaning time after every batch
for (k=0;k<NJ;k++) {
    if (k < NJ-1) {
        KEltTerm2D kelt(CLEAN,rank[k],rank[k+1]);
        problem.post(new KElement2D(kelt,clean[k],"element"));
    } else {
        KEltTerm2D kelt(CLEAN,rank[k],rank[0]);
        problem.post(new KElement2D(kelt,clean[k],"element"));
    }
}

// objective variable creation
cycleTime = new KIntVar(problem,"cycleTime",0,1000);

// Objective: minimize the duration of a production cycle
KLinTerm cycleTerm;
for (j=0;j<NJ;j++) {
    cycleTerm = cycleTerm + DUR[j];
}
KLinTerm cleanTerm;
for (k=0;k<NJ;k++) {
    cleanTerm = cleanTerm + clean[k];
}
problem.post(cycleTerm + cleanTerm == *cycleTime);

// One position for every job
problem.post(new KAllDifferent("alldiff",rank));

// propagating problem
if (problem.propagate()) {
    printf("Problem is infeasible\n");
    exit(1);
}

// Solve the problem
// creation of the solver
KSolver solver(problem);

// setting objective and sense of optimization
problem.setSense(KProblem::Minimize);
problem.setObjective(*cycleTime);

int result = solver.optimize();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();

// Solution printing
printf("Minimum cycle time: %i\n", sol->getValue(*cycleTime));
printf("Sequence of batches:\nBatch Duration Cleaning\n");
for (k=0;k<NJ;k++) {
    printf("%i\t%i\t%i\n", sol->getValue(rank[k]), DUR[sol->getValue(rank[k])], sol->getValue(clean[k]));
}

### Data
# Number of paint batches (=jobs)
nb_jobs = 5
# Durations of jobs
jobs_durations  = [40, 35, 45, 32, 50]

# Cleaning times between jobs
jobs_cleaning_times = [[0, 11, 7, 13, 11],
            [5, 0, 13, 15, 15],
            [13, 15, 0, 23, 11],
            [9, 13, 5, 0, 3],
            [3, 7, 7, 7, 0]]
max_cleaning_time = max(max(jobs_cleaning_times[j]) for j in range(nb_jobs))

# Setting data as a KIntMatrix
K_cleaning_times_matrix = KIntMatrix(5, 5, 0, "CLEAN")
for i in range(nb_jobs):
    for j in range(nb_jobs):
        K_cleaning_times_matrix.setMatrix(i, j, jobs_cleaning_times[i][j])

### Creation of the problem
# Creation of the Kalis session
session = KSession()

# Creation of the problem in this session
problem = KProblem(session, "B-5 Paint production")

### Variable creation
# Successor of a batch
batch_rank = KIntVarArray()
for j in range(nb_jobs):
    batch_rank += KIntVar(problem, "rank(%d)" % j, 0, nb_jobs - 1)

# Cleaning time after batches
batch_cleaning_time = KIntVarArray()
for j in range(nb_jobs):
    batch_cleaning_time += KIntVar(problem, "clean(%d)" % j, 0, max_cleaning_time)

### Constraints creation
# Set cleaning times after every batch
for k in range(nb_jobs):
    if k < nb_jobs - 1:
        kelt = KEltTerm2D(K_cleaning_times_matrix, batch_rank[k], batch_rank[k + 1])
        problem.post(KElement2D(kelt, batch_cleaning_time[k], "element"))
    else:
        kelt = KEltTerm2D(K_cleaning_times_matrix, batch_rank[k], batch_rank[0])
        problem.post(KElement2D(kelt, batch_cleaning_time[k], "element"))

# One position for every job
problem.post(KAllDifferent("alldiff", batch_rank))

# Set objective
cycle_time = KIntVar(problem, "cycle_time", 0, 1000)
batch_cleaning_times_sum = 0
for j in range(nb_jobs):
    batch_cleaning_times_sum += batch_cleaning_time[j]

problem.post(cycle_time == (batch_cleaning_times_sum + sum(jobs_durations)))

# First propagation to check inconsistency
if problem.propagate():
    print("Problem is infeasible")
    sys.exit(1)

### Solve the problem
# Set the solver
solver = KSolver(problem)

# Setting objective and sense of optimization
problem.setSense(KProblem.Minimize)
problem.setObjective(cycle_time)

# Run optimization
result = solver.optimize()
# Solution printing
if result:
    solution = problem.getSolution()
    solution.printResume()
    print("Minimum cycle time: %d" % solution.getValue(cycle_time))
    print("Sequence of batches:")
    print("Batch Duration Cleaning")
    for k in range(nb_jobs):
        job_id = solution.getValue(batch_rank[k])
        print("%d\t%d\t%d" % (job_id, jobs_durations[job_id],
                 solution.getValue(batch_cleaning_time[k])))

// Cleaning times between jobs
KIntMatrix CLEAN = new KIntMatrix(5, 5, 0, "CLEAN");
CLEAN.setMatrix(0, 0, 0);
CLEAN.setMatrix(1,0,11);
CLEAN.setMatrix(2,0,7);
CLEAN.setMatrix(3,0,13);
CLEAN.setMatrix(4,0,11);
CLEAN.setMatrix(0,1,5);
CLEAN.setMatrix(1,1,0);
CLEAN.setMatrix(2,1,13);
CLEAN.setMatrix(3,1,15);
CLEAN.setMatrix(4,1,15);
CLEAN.setMatrix(0,2,13);
CLEAN.setMatrix(1,2,15);
CLEAN.setMatrix(2,2,0);
CLEAN.setMatrix(3,2,23);
CLEAN.setMatrix(4,2,11);
CLEAN.setMatrix(0,3,9);
CLEAN.setMatrix(1,3,13);
CLEAN.setMatrix(2,3,5);
CLEAN.setMatrix(3,3,0);
CLEAN.setMatrix(4,3,3);
CLEAN.setMatrix(0,4,3);
CLEAN.setMatrix(1,4,7);
CLEAN.setMatrix(2,4,7);
CLEAN.setMatrix(3,4,7);
CLEAN.setMatrix(4,4,0);

// Successor of a batch
KIntVarArray rank = new KIntVarArray();
// Cleaning time after batches
KIntVarArray clean = new KIntVarArray();
// Objective variable
KIntVar cycleTime = new KIntVar();

// Creation of the problem in this session
KProblem problem = new KProblem(session, "B-5 Paint production");

// variables creation
int k,j;
for (j=0; j<NJ; j++)
{
    rank.add(new KIntVar(problem, "rank(" + j + ")", 0, NJ-1) );
    clean.add(new KIntVar(problem, "clean(" + j + ")", 0, 1000) );
}

// Cleaning time after every batch
for (k=0; k<NJ; k++)
{
    if (k < NJ-1)
    {
        KEltTerm2D kelt = new KEltTerm2D(CLEAN, rank.getElt(k), rank.getElt(k+1));
        problem.post(new KElement2D(kelt, clean.getElt(k), "element"));
    } else {
        KEltTerm2D kelt = new KEltTerm2D(CLEAN, rank.getElt(k), rank.getElt(0));
        problem.post(new KElement2D(kelt, clean.getElt(k), "element"));
    }
}

// objective variable creation
cycleTime = new KIntVar(problem, "cycleTime", 0, 1000);

// Objective: minimize the duration of a production cycle
KLinTerm cleanTerm = new KLinTerm();
int sumOfDUR = 0;

for (j=0; j<NJ; j++)
{
    cleanTerm.add(clean.getElt(j),1);
    sumOfDUR += DUR[j];
}

KNumVarArray intVarArrayToSet = cleanTerm.getLvars();
KDoubleArray coeffsToSet = cleanTerm.getCoeffs();
intVarArrayToSet.add(cycleTime);
coeffsToSet.add(-1);
problem.post(new KNumLinComb("",coeffsToSet,intVarArrayToSet,sumOfDUR,KNumLinComb.LinCombOperator.Equal));

// One position for every job
problem.post(new KAllDifferent("alldiff",rank));

// propagating problem
if (problem.propagate())
{
    System.out.println("Problem is infeasible");
    exit(1);
}

// Solve the problem
// creation of the solver
KSolver solver = new KSolver(problem);

// setting objective and sense of optimization
problem.setSense(KProblem.Sense.Minimize);
problem.setObjective(cycleTime);

solver.optimize();
// solution printing
KSolution sol = problem.getSolution();
// print solution resume
sol.printResume();

// Solution printing
System.out.println("Minimum cycle time: " + sol.getValue(cycleTime));
System.out.print("Sequence of batches:\nBatch Duration Cleaning\n");
for (k=0; k<NJ; k++)
{
    System.out.print(sol.getValue(rank.getElt(k)) + "\t" + DUR[sol.getValue(rank.getElt(k))] + "\t" + sol.getValue(clean.getElt(k)) + "\n");
}

Results¶

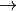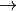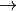The minimum cycle time for this problem is 243 minutes which is achieved with the following sequence of batches: 1 $\rightarrow$ 2 $\rightarrow$ 5 $\rightarrow$ 3 $\rightarrow$ 4 $\rightarrow$ 1. This time includes 202 minutes of (incompressible) processing time and 41 minutes of cleaning.