Assignment with task sizes¶

Problem description¶

In this example, 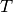$T$ tasks must be assigned to 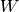$W$ workers. Each task has a specific size which represents how much time or effort is required. A worker can have as many tasks as the total size of its tasks is below a fixed bound 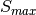$S_{max}$ . The cost of a task is a function of the worker to which it is assigned.

The aim is to minimize the total cost.

Naive modelling¶

The problem can be exposed as follows:

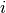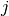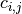Let $(X_{i,j})_{(i,j) \in [|1,T|]\times[|1,W|]}$ be the set of binary variables indicating whether task $i$ has been assigned to worker $j$ . Let $(S_{i})_{i \in [|1,T|]}$ be the set of integers representing the size of the tasks. Let $C = (c_{i,j})_{(i,j) \in [|1,T|]\times[|1,W|]}$ with $c_{i,j}$ the cost associated with the assignment of task 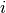$i$ . to worker $j$ .

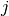The problem is then:

$& \text{ minimize } \sum_{(i,j) \in [|1,T|]\times[|1,W|]} X_{i,j} \times c_{i,j} \\ & \\ & \text{ s.t } \\ &\forall i \in [|1,T|], \sum_{j \in [|1,W|]} X_{i,j} = 1 \\ &\forall j \in [|1,W|], \sum_{i \in [|1,T|]} X_{i,j} \times S_{i} \leq S_{max} \\$

This description, despite its ability to be easily understood, is not very effective. Two other more efficient implementations are presented in this section.

Implementation with standard API¶

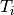Since a a worker can have several tasks assigned to him, it is not possible to use variables $(W_{i})_{i \in [1,W]}$ giving the task assigned to each worker. The variables have to be $(T_{i})_{i \in [1,T]}$ with $T_{i}$ the worker assigned to task $i$ .

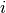Those variables ensure that each task is assigned once. The only remaining constraint is the capacity constraint on each worker.

A modelling trick is to create an array of variable in which for all 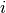$i$ the variable 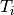$T_{i}$ is present as many times as its size. The number of times the number of a worker appears in this array is then equals to the total size of tasks assigned to him and it can be expressed through a cardinality constraint.

This solution can be implemented as follows:

from itertools import chain

def solve(cost_matrix: list, tasks_size: list, worker_size_max: int):
    """ Resolution of the assignment with task sizes problem """

    # Get the number of tasks and workers from cost_matrix
    nb_task = len(cost_matrix[1])
    nb_worker = len(cost_matrix)

    try:

        # Declaration of the problem
        session = KSession()
        problem = KProblem(session, "assignment_with_task_sizes")

        # Variables declaration
        worker_assigned_to_task = KIntVarArray()

        # Initialize variables giving the task assigned to each one of them. Last task is idle.
        for task in range(nb_task):
            worker_assigned_to_task += KIntVar(problem, "worker_assigned_to_{}".format(task), 0, nb_worker - 1)

        # Declaration of an array in which the variable of each task is present as many times as its size
        expanded_worker_assigned_to_task = KIntVarArray()
        for task in range(nb_task):
            for i in range(tasks_size[task]):
                expanded_worker_assigned_to_task += worker_assigned_to_task[task]

        # Constraint declaration
        # Assert that each worker has a total amount of task's size below worker_size_max by counting how many times it
        # appears in array expanded_worker_assigned_to_task
        for worker in range(nb_worker):
            problem.post(KOccurTerm(worker, expanded_worker_assigned_to_task) <= worker_size_max)

        # Objective declaration
        # Transform the cost matrix into a Kalis object
        K_cost_matrix = KIntMatrix(nb_worker, nb_task, 0, "cost_matrix")
        for worker in range(nb_worker):
            for task in range(nb_task):
                K_cost_matrix.setMatrix(worker, task, int(cost_matrix[worker][task]))

        # Objective will be greater than nb_task times the minimum of cost_matrix and lower than the sum of the
        # coefficients in cost_matrix
        objective_sup = sum(chain(*cost_matrix))
        objective_inf = nb_task * min(chain(*cost_matrix))

        # Get the cost of the tasks given the worker they are assigned to
        cost_task = KIntVarArray()
        K_cost_worker, K_elt = {}, {}
        for task in range(nb_task):
            K_cost_worker[task] = KIntArray()
            for worker in range(nb_worker): K_cost_worker[task] += int(cost_matrix[worker][task])

            cost_task += KIntVar(problem, "Cost_{}".format(task),
                                 0, max([cost_matrix[worker][task] for worker in range(nb_worker)]))
            K_elt[task] = KEltTerm(K_cost_worker[task], worker_assigned_to_task[task])
            problem.post(KElement(K_elt[task], cost_task[task]))

        # The objective is the sum of those costs
        objective = KIntVar(problem, "cost", int(objective_inf), int(objective_sup))
        problem.post(objective == sum(cost_task[task] for task in range(nb_task)))

        # Set the objective
        problem.setSense(KProblem.Minimize)
        problem.setObjective(objective)

        # Set the solver
        solver = KSolver(problem)

        # If the problem is infeasible
        if problem.propagate():
            # Display various details to help find the source of the problem
            problem.display()
            problem.printMinimalConflictSet()
            print("Problem is infeasible")
            exit()

        # Launch the optimization
        result = solver.optimize()
        if result:
            solution = problem.getSolution()
            # Display the solution
            for task in range(nb_task): print(
                f'Task {task} has been affected to worker {solution.getValue(worker_assigned_to_task[task])} '
                f'with cost {solution.getValue(cost_task[task])}')
            print(f'Total cost : {solution.getValue(objective)}')

            # Return the objective
            problem.getSolution().display()
            return solution.getValue(objective)

    except ArtelysException as e:
        print(e)


if __name__ == '__main__':
    COST = [[90, 76, 75, 70, 50, 74, 12, 68],
            [35, 85, 55, 65, 48, 101, 70, 83],
            [125, 95, 90, 105, 59, 120, 36, 73],
            [45, 110, 95, 115, 104, 83, 37, 71],
            [60, 105, 80, 75, 59, 62, 93, 88],
            [45, 65, 110, 95, 47, 31, 81, 34],
            [38, 51, 107, 41, 69, 99, 115, 48],
            [47, 85, 57, 71, 92, 77, 109, 36],
            [39, 63, 97, 49, 118, 56, 92, 61],
            [47, 101, 71, 60, 88, 109, 52, 90]]

    SIZES = [10, 7, 3, 12, 15, 4, 11, 5]
    TOTAL_MAX_SIZES = 15

    solve(COST, SIZES, TOTAL_MAX_SIZES)

Implementation with scheduling API¶

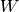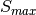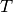Even if the problem does not have a time dimension, it is possible to use the scheduling API to implement it. By considering a time period of $[0, W]$ , with $W$ the number of workers, a single ressource with a capacity of $S_{max}$ , and $T$ tasks, the statment ‘task i start at j’ can be assimilated to the statment ‘task i has been assigned to worker j’.

By making each task require 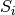$S_{i}$ unit of capacity from the ressource, it is possible to ensure that the size limit is respected.

A way to implement this method is as follows :

from itertools import chain

def solve(cost_matrix: list, tasks_size: list, worker_size_max: int):
    """ Resolution of the task size problem """

    # Get the number of tasks and workers from the cost matrix
    nb_task = len(cost_matrix[1])
    nb_worker = len(cost_matrix)

    try:

        # Declaration of the problem
        session = KSession()
        problem = KProblem(session, "task_size")

        # Creation of the schedule object with time horizon (0..nb_worker). The start date of a task will then be the
        # number of the worker it is allocated to
        schedule = KSchedule(problem, "schedule", 0, nb_worker)

        # Setting up the resource which are the workers. They are discrete because a worker can take on several task,
        # it has a capacity of worker_size_max.
        workers = KDiscreteResource(schedule, "workers", worker_size_max)

        # Setting up the tasks_array. Each task has a length of 1 - it requires only one worker - and has its on value
        # for the workers capacity consumption
        tasks_array = KTaskArray()
        for task in range(nb_task):
            tasks_array += KTask(schedule, "Task_{}".format(task), 1)
            tasks_array[task].requires(workers, int(tasks_size[task]))

        # Objective declaration
        # Transform the cost matrix into a Kalis object
        K_cost_matrix = KIntMatrix(nb_worker, nb_task, 0, "cost")
        for worker in range(nb_worker):
            for task in range(nb_task):
                K_cost_matrix.setMatrix(worker, task, int(cost_matrix[worker][task]))

        # The objective will be greater than nb_task times the minimum of cost_matrix and lower than the sum of the
        # coefficients in cost_matrix
        objective_sup = sum(chain(*cost_matrix))
        objective_inf = nb_task * min(chain(*cost_matrix))

        # Get the cost of the task given the worker they are assigned to
        cost_task = KIntVarArray()
        K_cost_worker, K_elt = {}, {}
        for task in range(nb_task):
            K_cost_worker[task] = KIntArray()
            for worker in range(nb_worker): K_cost_worker[task] += int(cost_matrix[worker][task])

            cost_task += KIntVar(problem, "Cost_{}".format(task),
                                 0, max([cost_matrix[worker][task] for worker in range(nb_worker)]))
            K_elt[task] = KEltTerm(K_cost_worker[task], tasks_array[task].getStartDateVar())
            problem.post(KElement(K_elt[task], cost_task[task]))

        # The objective is the sum of those costs
        objective = KIntVar(problem, "cost", int(objective_inf), int(objective_sup))
        problem.post(objective == sum(cost_task[task] for task in range(nb_task)))

        # Set the objective
        schedule.close()
        problem.setSense(KProblem.Minimize)
        problem.setObjective(objective)

        # Set the solver
        solver = KSolver(problem)

        # If the problem is infeasible
        if problem.propagate():
            # Display of various details to help find the source of the problem
            problem.display()
            problem.printMinimalConflictSet()
            print("Problem is infeasible")
            exit()

        # Launch the optimization
        result = solver.optimize()
        if result:
            solution = problem.getSolution()
            # Display the solution
            for task in range(nb_task): print(
                f'Task {task} has been affected to worker {solution.getValue(tasks_array[task].getStartDateVar())} '
                f'with cost {solution.getValue(cost_task[task])}')
            print(f'Total cost : {solution.getValue(objective)}')

            # Return the objective
            problem.getSolution().display()
            return solution.getValue(objective)


    except ArtelysException as e:
        print(e)


if __name__ == '__main__':
    COST = [[90, 76, 75, 70, 50, 74, 12, 68],
            [35, 85, 55, 65, 48, 101, 70, 83],
            [125, 95, 90, 105, 59, 120, 36, 73],
            [45, 110, 95, 115, 104, 83, 37, 71],
            [60, 105, 80, 75, 59, 62, 93, 88],
            [45, 65, 110, 95, 47, 31, 81, 34],
            [38, 51, 107, 41, 69, 99, 115, 48],
            [47, 85, 57, 71, 92, 77, 109, 36],
            [39, 63, 97, 49, 118, 56, 92, 61],
            [47, 101, 71, 60, 88, 109, 52, 90]]

    SIZES = [10, 7, 3, 12, 15, 4, 11, 5]
    TOTAL_MAX_SIZES = 15

    solve(COST, SIZES, TOTAL_MAX_SIZES)