Task assignment problem¶

The problem consists in finding a sequence of starting times of various activities, namely 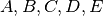$A,B,C,D,E$ , of a given plant. Each activity got 5 different time slots for its starting time, represented by the set 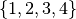$\{1,2,3,4\}$ . Due to some plant requirements, two-by-two constraints exists upon the starting time activities :

B can’t begin at 3 ;
C can’t begin at 2 ;
A and B can’t begin at the same starting time ;
B and C can’t begin at the same starting time ;
C must begin after D ;
E must begin after A ;
E must begin after B ;
E must begin after C ;
E must begin after D ;
B and D can’t begin at the same starting time ;
A and D must begin at the same time.

Model formulation¶

To represent the activities starting time we defined as many variables as activities 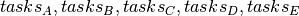$tasks_A, tasks_B, tasks_C, tasks_D, tasks_E$ , with a domain of integer from 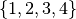$\{1,2,3,4\}$ . Constraints can be expressed as implicit constraints but also through a global constraint : a generic arc-consistency (GAC) constraint. It mainly proceeds by examining the arcs between tuples of variables and removes those values from its domain which aren’t consistent with the constraint.

The implicit constraints can be written as :

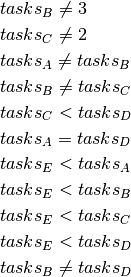
$& tasks_B \neq 3 \\ & tasks_C \neq 2 \\ & tasks_A \neq tasks_B \\ & tasks_B \neq tasks_C \\ & tasks_C < tasks_D \\ & tasks_A = tasks_D \\ & tasks_E < tasks_A \\ & tasks_E < tasks_B \\ & tasks_E < tasks_C \\ & tasks_E < tasks_D \\ & tasks_B \neq tasks_D \\$

And they can be expressed through a test function that validate or not a given starting time combination:

bool StartingTimeCombinationOk(int a, int b, int c, int d, int e) {
    return (b!=3) && (c!=2) && (a!=b) && (b!=c) && (c<d) && (a=d) && (e<a) && (e<b) && (e<c) && (e<d) && (b!=d);
}

def StartingTimeCombinationOk(a, b, c, d, e):
    return (b != 3) and (c != 2) and (a != b) and (b != c) and (c < d) and (a == d) and \
        (e < a) and (e < b) and (e < c) and (e < d) and (b != d)

// todo

The GAC constraint can be implemented through both classes KGeneralizedArcConsistencyConstraint and KGeneralizedArcConsistencyTableConstraint. Difference relies on the way the test function is used in the implementation of the constraint, and therefore the propagation algorithm behind.

Implementation of the GAC constraint¶

In the standard version of the GAC constraint, end-user needs to create a derived class of KGeneralizedArcConsistencyConstraint which mainly overloads the testIfSatisfied() (constructor and copy-constructor are also needed). The former method is used by the propagation engine to test all valid combinations defined by the domain of variables. testIfSatisfied() is called each time one tuple needs to be validated.

class StartingTimeCombination : public KGeneralizedArcConsistencyConstraint {
public:
    KIntVarArray _vars;

    StartingTimeCombination(KIntVarArray& vars)
    : KGeneralizedArcConsistencyConstraint(vars,GENERALIZED_ARC_CONSISTENCY, "StartingTimeCombinationGAC"),_vars(vars)
    {}

    ~StartingTimeCombination() {
    }

    bool testIfSatisfied(int * vals)
    {
    int _a = vals[1];int _b = vals[2];int _c = vals[3];int _d = vals[4];int _e = vals[5];

    return StartingTimeCombinationOk(_a, _b, _c, _d, _e);
    }

    StartingTimeCombination(const StartingTimeCombination& toCopy) : KGeneralizedArcConsistencyConstraint(toCopy)
    {
        _vars = KIntVarArray(toCopy._vars);
    }
};

class StartingTimeCombination(KGeneralizedArcConsistencyConstraint):
    """This class ineherits from the KACBinConstraint and allow to define a custom binary
    arc-consistency constraint."""

    def __init__(self, vars):
        """Initialize the StartingTimeCombinationGAC constraint."""
        KGeneralizedArcConsistencyConstraint.__init__(self, vars,
                                                    KGeneralizedArcConsistencyConstraint.GENERALIZED_ARC_CONSISTENCY,
                                                    "StartingTimeCombinationGAC")
        self.vars = vars

    def testIfSatisfied(self, values):
        """Overload the 'testIfSatisfied' method in 'KGeneralizedArcConsistencyConstraint' class by using a user
        defined function. """
        return StartingTimeCombinationOk(*values)

// todo

Finally the complete task assignment example implementation is :

class StartingTimeCombination : public KGeneralizedArcConsistencyConstraint {
  public:
    KIntVarArray _vars;

    StartingTimeCombination(KIntVarArray& vars)
    : KGeneralizedArcConsistencyConstraint(vars,GENERALIZED_ARC_CONSISTENCY, "StartingTimeCombinationGAC"),_vars(vars)
    {}

    ~StartingTimeCombination() {
    }

    bool testIfSatisfied(int * vals)
    {
    int _a = vals[1];int _b = vals[2];int _c = vals[3];int _d = vals[4];int _e = vals[5];

    return StartingTimeCombinationOk(_a, _b, _c, _d, _e);
    }

    StartingTimeCombination(const StartingTimeCombination& toCopy) : KGeneralizedArcConsistencyConstraint(toCopy)
    {
        _vars = KIntVarArray(toCopy._vars);
    }


};

/////////////////////////////////////////////
// Task activities starting time
/////////////////////////////////////////////
enum TASKS {A,B,C,D,E};
const char * TaskName[] = {"A","B","C","D","E"};
int N=5;

KIntVarArray tasks;

/////////////////////////////////////////////
// Create the task activities variables
/////////////////////////////////////////////
char name[80];
int indexTask;
for (indexTask = A; indexTask <= E; indexTask++) {
    sprintf(name,"task[%s]",TaskName[indexTask]);
    tasks += KIntVar(problem,name,1,4);
}

///////////////////////////////////////////////
// the task activities should follow the combination rules
///////////////////////////////////////////////

StartingTimeCombination gacConstraint(tasks);
problem.post(gacConstraint);

/////////////////////////////////////////////
// Solve the problem
// creation of the solver
/////////////////////////////////////////////
KSolver solver(problem);

/////////////////////////////////////////////
// propagating problem
/////////////////////////////////////////////
if (problem.propagate()) {
    printf("Problem is infeasible\n");
    return 1;
}

solver.solve();

/////////////////////////////////////////////
// solution printing
/////////////////////////////////////////////
KSolution * sol = &problem.getSolution();

/////////////////////////////////////////////
// print solution resume
/////////////////////////////////////////////
sol->printResume();

cout << "### Computation time = " << solver.getDblAttrib(KSolver::ComputationTime) << endl;
cout << "### Number of nodes = " << solver.getIntAttrib(KSolver::NumberOfNodes) << endl;
cout << "### Depth = " << solver.getIntAttrib(KSolver::Depth) << endl;

return 0;
}

def modelisation_using_GACConstraint(problem):
    # Task activities starting time
    task_idx = {"A": 0, "B": 1, "C": 2, "D": 3, "E": 4}
    tasks = KIntVarArray()

    # Create the task activities variables
    for name in task_idx:
        tasks += KIntVar(problem, f"task[{name}]", 1, 4)

    # the task activities should follow the combination rules
    gacConstraint = StartingTimeCombination(tasks)
    problem.post(gacConstraint)

    # Solve the problem
    solver = KSolver(problem)

    # propagating problem
    if problem.propagate():
        print("Problem is infeasible")
        exit()

    solver.solve()

    # solution printing
    sol = problem.getSolution()

    # print solution resume
    sol.printResume()

    print(f"### Computation time = {solver.getDblAttrib(KSolver.ComputationTime)}")
    print(f"### Number of nodes = {solver.getIntAttrib(KSolver.NumberOfNodes)}")
    print(f"### Depth = {solver.getIntAttrib(KSolver.Depth)}")

// todo

Implementation of the GAC Table constraint¶

In the following GAC constraint (KGeneralizedArcConsistencyTableConstraint version), end-user needs this time to enumerate the complete list of valid tuples that defined the valid support of the variables with respect to the constraint. This list of tuple will be used by the propagation engine to filter the domain variables, as it is done with testIfSatisfied() in KGeneralizedArcConsistencyConstraint. This implementation is identified as the one to be preferred when the list of valid tuples is greatly inferior to the overall combinatorial of the variables.

The implementation is:

/////////////////////////////////////////////
// Task activities starting time
/////////////////////////////////////////////
enum TASKS {A,B,C,D,E};
const char * TaskName[] = {"A","B","C","D","E"};
int N=5;

KIntVarArray tasks;

/////////////////////////////////////////////
// Create the task activities variables
/////////////////////////////////////////////
char name[80];
int indexTask;
for (indexTask = A; indexTask <= E; indexTask++) {
    sprintf(name,"task[%s]",TaskName[indexTask]);
    tasks += KIntVar(problem,name,1,4);
}

///////////////////////////////////////////////
// the task activities should follow the combination rules
///////////////////////////////////////////////
KTupleArray tuple;
int _a, _b, _c, _d, _e;
for (_a = 0; _a <= 4; _a++) for (_b = 0; _b <= 4; _b++) for (_c = 0; _c <= 4; _c++) for (_d = 0; _d <= 4; _d++) for (_e = 0; _e <= 4; _e++) {
    if (StartingTimeCombinationOk(_a, _b, _c, _d, _e)) {
        KIntArray tuple_elem(N);
        tuple_elem[A] = _a; tuple_elem[B] = _b; tuple_elem[C] = _c; tuple_elem[D] = _d; tuple_elem[E] = _e;
        tuple.add(tuple_elem);
    }
}

KGeneralizedArcConsistencyTableConstraint gacTableConstraint(tasks, tuple,"StartingTimeCombinationGACTable");
problem.post(gacTableConstraint);

/////////////////////////////////////////////
// Solve the problem
// creation of the solver
/////////////////////////////////////////////
KSolver solver(problem);

/////////////////////////////////////////////
// propagating problem
/////////////////////////////////////////////
if (problem.propagate()) {
    printf("Problem is infeasible\n");
    return 1;
}

solver.solve();

/////////////////////////////////////////////
// solution printing
/////////////////////////////////////////////
KSolution * sol = &problem.getSolution();

/////////////////////////////////////////////
// print solution resume
/////////////////////////////////////////////
sol->printResume();

cout << "### Computation time = " << solver.getDblAttrib(KSolver::ComputationTime) << endl;
cout << "### Number of nodes = " << solver.getIntAttrib(KSolver::NumberOfNodes) << endl;
cout << "### Depth = " << solver.getIntAttrib(KSolver::Depth) << endl;

return 0;

def modelisation_using_GACTableConstraint(problem):
    # Task activities starting time
    task_idx = {"A": 0, "B": 1, "C": 2, "D": 3, "E": 4}
    tasks = KIntVarArray()

    # Create the task activities variables
    for name in task_idx:
        tasks += KIntVar(problem, f"task[{name}]", 1, 4)

    # the task activities should follow the combination rules
    K_tuple = KTupleArray()
    for (_a, _b, _c, _d, _e) in product(range(1, 6, 1), repeat=5):
        if StartingTimeCombinationOk(_a, _b, _c, _d, _e):
            K_tuple_elem = KIntArray()
            K_tuple_elem += _a
            K_tuple_elem += _b
            K_tuple_elem += _c
            K_tuple_elem += _d
            K_tuple_elem += _e
            K_tuple += K_tuple_elem

    gacTableConstraint = KGeneralizedArcConsistencyTableConstraint(tasks, K_tuple, "StartingTimeCombinationGACTable")
    problem.post(gacTableConstraint)

    # Solve the problem
    solver = KSolver(problem)

    # propagating problem
    if problem.propagate():
        print("Problem is infeasible")
        exit()

    solver.solve()

    # solution printing
    sol = problem.getSolution()

    # print solution resume
    sol.printResume()

    print(f"### Computation time = {solver.getDblAttrib(KSolver.ComputationTime)}")
    print(f"### Number of nodes = {solver.getIntAttrib(KSolver.NumberOfNodes)}")
    print(f"### Depth = {solver.getIntAttrib(KSolver.Depth)}")

// todo