Sequencing jobs on a single machine¶
The problem described in this section is taken from Section 7.4 Sequencing jobs on a bottleneck machine of the book Applications of optimization with Xpress-MP. The aim of this problem is to provide a model that may be used with different objective functions for scheduling operations on a single (bottleneck) machine. We shall see here how to minimize the total processing time, the average processing time, and the total tardiness. A set of tasks (or jobs) is to be processed on a single machine. The execution of tasks is nonpreemptive (that is, an operation may not be interrupted before its completion). For every task 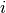 its release date, duration, and due date are given in the following table :
its release date, duration, and due date are given in the following table :
Job |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Release date |
2 |
5 |
4 |
0 |
0 |
8 |
9 |
Duration |
5 |
6 |
8 |
4 |
2 |
4 |
2 |
Due date |
10 |
21 |
15 |
10 |
5 |
15 |
22 |
What is the optimal value for each of the objectives: minimizing the total duration of the schedule (makespan), the mean processing time or the total tardiness (that is, the amount of time by which the completion of jobs exceeds their respective due dates) ?
Model formulation¶
We are going to present a model formulation that is close to the Mathematical Programming formulation in Applications of optimization with Xpress-MP. In model formulation we are going to deal with the different objective functions in sequence, but the body of the models will remain the same. To represent the sequence of jobs we introduce variables 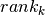 with
with 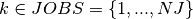 that take as value the number of the job in position (rank)
that take as value the number of the job in position (rank) 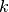 . Every job
. Every job 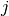 takes a single position. This constraint can be represented by a
takes a single position. This constraint can be represented by a KAllDifferent on the 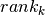 variables:
variables:
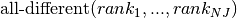
The processing time 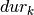 for the job in position
for the job in position 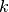 is given by
is given by 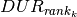 (where
(where 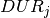 denotes the duration given in the table in the previous section). Similarly, the release time
denotes the duration given in the table in the previous section). Similarly, the release time 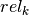 is given by
is given by 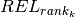 (where
(where 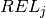 denotes the given release date):
denotes the given release date):
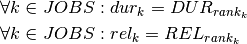
If 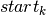 is the start time of the job at position
is the start time of the job at position 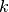 , this value must be at least as great as the release date of the job assigned to this position. The completion time
, this value must be at least as great as the release date of the job assigned to this position. The completion time 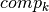 of this job is the sum of its start time plus its duration:
of this job is the sum of its start time plus its duration:
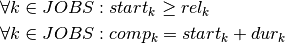
Another constraint is needed to specify that two jobs cannot be processed simultaneously. The job in position 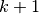 must start after the job in position
must start after the job in position 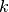 has finished, hence the following
constraints:
has finished, hence the following
constraints:
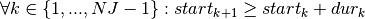
Objective 1: The first objective is to minimize the makespan (completion time of the schedule), or, equivalently, to minimize the completion time of the last job (job with rank 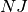 ). The complete model is then given by the following (where
). The complete model is then given by the following (where 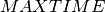 is a sufficiently large value, such as the sum of all release dates and all durations):
is a sufficiently large value, such as the sum of all release dates and all durations):
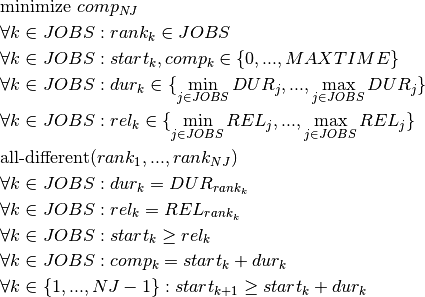
Objective 2: For minimizing the average processing time, we introduce an additional variable 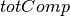 representing the sum of the completion times of all jobs. We add the following constraint to the problem to calculate
representing the sum of the completion times of all jobs. We add the following constraint to the problem to calculate 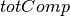 :
:
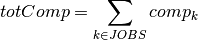
The new objective consists of minimizing the average processing time, or equivalently, minimizing the sum of the job completion times: 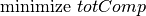
Objective 3: If we now aim to minimize the total tardiness, we again introduce new variables this time to measure the amount of time that jobs finish after their due date. We write 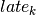 for the variable that corresponds to the tardiness of the job with rank
for the variable that corresponds to the tardiness of the job with rank 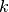 . Its value is the difference between the completion time of a job
. Its value is the difference between the completion time of a job 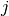 and its due date
and its due date 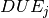 . If the job finishes before its due date, the value must be zero. We thus obtain the following constraints:
. If the job finishes before its due date, the value must be zero. We thus obtain the following constraints:
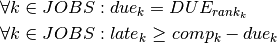
For the formulation of the new objective function we introduce the variable  representing the total tardiness of all jobs. The objective now is to minimize the value of this variable:
representing the total tardiness of all jobs. The objective now is to minimize the value of this variable:
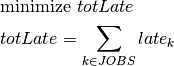
Implementation¶
The implementation below (BottleneckSequencing.cpp) solves the same problem three times, each time with a different objective, and prints the resulting solutions.
// Number of tasks
int NTASKS = 7;
// Release date of tasks
int REL[] = { 2, 5, 4, 0, 0, 8, 9};
// Duration of tasks
int DUR[] = { 5, 6, 8, 4, 2, 4, 2};
// Due date of tasks
int DUE[] = {10, 21, 15, 10, 5, 15, 22};
// Number of job at position k
KIntVarArray rank;
// Start time of job at position k
KIntVarArray start;
// Duration of job at position k
KIntVarArray dur;
// Completion time of job at position k
KIntVarArray comp;
// Release date of job at position k
KIntVarArray rel;
// Creation of the problem in this session
KProblem problem(session,"B-4 Sequencing");
// compute some statistics
int indexTask;
int MAXTIME = 0;
int MINDUR = MAX_INT;
int MAXDUR = 0;
int MINREL = MAX_INT;
int MAXREL = 0;
int MINDUE = MAX_INT;
int MAXDUE = 0;
int SDUR = 0;
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
if (MINDUR > DUR[indexTask]) {
MINDUR = DUR[indexTask];
}
if (MAXDUR < DUR[indexTask]) {
MAXDUR = DUR[indexTask];
}
if (MINREL > REL[indexTask]) {
MINREL = REL[indexTask];
}
if (MAXREL < REL[indexTask]) {
MAXREL = REL[indexTask];
}
if (MINDUE > DUE[indexTask]) {
MINDUE = DUE[indexTask];
}
if (MAXDUE < DUE[indexTask]) {
MAXDUE = DUE[indexTask];
}
SDUR += DUR[indexTask];
}
MAXTIME = MAXREL + SDUR;
char name[80];
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"rank(%i)",indexTask);
rank += (* new KIntVar(problem,name,0,NTASKS-1));
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"start(%i)",indexTask);
start += (* new KIntVar(problem,name,0,MAXTIME));
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"dur(%i)",indexTask);
dur += (* new KIntVar(problem,name,MINDUR,MAXDUR));
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"comp(%i)",indexTask);
comp += (* new KIntVar(problem,name,0,MAXTIME));
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"rel(%i)",indexTask);
rel += (* new KIntVar(problem,name,MINREL,MAXREL));
}
// One position per job
problem.post(KAllDifferent("alldiff(rank)",rank));
// Duration of job at position k
KIntArray idur;
KIntArray irel;
KIntArray idue;
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
idur += DUR[indexTask];
irel += REL[indexTask];
idue += DUE[indexTask];
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
KEltTerm kelt(idur,rank[indexTask]);
problem.post(kelt == dur[indexTask]);
// Release date of job at position k
KEltTerm keltrel(irel,rank[indexTask]);
problem.post(keltrel == rel[indexTask]);
}
for (indexTask = 0;indexTask < NTASKS-1; indexTask++) {
// Sequence of jobs
problem.post(start[indexTask+1] >= start[indexTask] + dur[indexTask]);
}
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
// Start times
problem.post(start[indexTask] >= rel[indexTask]);
// Completion times
problem.post(comp[indexTask] == start[indexTask] + dur[indexTask]);
}
// propagating problem
if (problem.propagate()) {
printf("Problem is infeasible\n");
exit(1);
}
// Set the branching strategy
KBranchingSchemeArray myBa;
myBa += KSplitDomain(KSmallestDomain(),KMinToMax());
// creation of the solver
KSolver solver(problem,myBa);
// **********************
// Objective 1: Makespan
// **********************
problem.setObjective(comp[NTASKS-1]);
problem.setSense(KProblem::Minimize);
// look for all solutions
int result = solver.optimize();
// solution printing
KSolution * sol = &problem.getSolution();
// print solution resume
sol->printResume();
// solution printing
printf("Completion time: %i\n",problem.getSolution().getValue(comp[NTASKS-1]));
printf("Rel\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",REL[indexTask]);
}
printf("\nDur\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUR[indexTask]);
}
printf("\nStart\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(start[indexTask]));
}
printf("\nEnd\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(comp[indexTask]));
}
printf("\nDue\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUE[indexTask]);
}
printf("\n");
// ***************************************
// Objective 2: Average completion time:
// ***************************************
KLinTerm totalCompletionTerm;
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
totalCompletionTerm = totalCompletionTerm + comp[indexTask];
}
KIntVar averageCompletion(problem,"average completion",0,1000);
problem.post(averageCompletion == totalCompletionTerm);
problem.setObjective(averageCompletion);
result = solver.optimize();
// solution printing
printf("Completion time: %i\n",problem.getSolution().getValue(comp[NTASKS-1]));
printf("average: %i\n",problem.getSolution().getValue(averageCompletion));
printf("Rel\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",REL[indexTask]);
}
printf("\nDur\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUR[indexTask]);
}
printf("\nStart\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(start[indexTask]));
}
printf("\nEnd\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(comp[indexTask]));
}
printf("\nDue\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUE[indexTask]);
}
printf("\n");
// *****************************
// Objective 3: total lateness:
// *****************************
// Lateness of job at position k
KIntVarArray late;
// Due date of job at position k
KIntVarArray due;
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
sprintf(name,"due(%i)",indexTask);
due += (* new KIntVar(problem,name,MINDUE,MAXDUE));
sprintf(name,"late(%i)",indexTask);
late += (* new KIntVar(problem,name,0,MAXTIME));
}
// Due date of job at position k
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
KEltTerm keltdue(idue,rank[indexTask]);
problem.post(keltdue == due[indexTask]);
}
KLinTerm totLatTerm;
// building each tasks with fixed time horizon (0..HORIZON)
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
// Late jobs: completion time exceeds the due date
problem.post(late[indexTask] >= (comp[indexTask]) - due[indexTask]);
totLatTerm = totLatTerm + late[indexTask];
}
KIntVar totLate(problem,"total lateness",0,1000);
problem.post(totLate == totLatTerm);
problem.setObjective(totLate);
result = solver.optimize();
// solution printing
printf("Completion time: %i\n",problem.getSolution().getValue(comp[NTASKS-1]));
printf("average: %i\n",problem.getSolution().getValue(averageCompletion));
printf("Tardiness: %i\n",problem.getSolution().getValue(totLate));
printf("Rel\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",REL[indexTask]);
}
printf("\nDur\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUR[indexTask]);
}
printf("\nStart\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(start[indexTask]));
}
printf("\nEnd\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(comp[indexTask]));
}
printf("\nDue\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",DUE[indexTask]);
}
printf("\nLate\t");
for (indexTask = 0;indexTask < NTASKS; indexTask++) {
printf("%i\t",problem.getSolution().getValue(late[indexTask]));
}
printf("\n");
import sys
from kalis import *
### Data creation
nb_tasks = 7
release_dates = [2, 5, 4, 0, 0, 8, 9]
durations = [5, 6, 8, 4, 2, 4, 2]
due_dates = [10, 21, 15, 10, 5, 15, 22]
### Variable creation
# Tasks positions
rank = KIntVarArray()
# Jobs starting dates
jobs_start = KIntVarArray()
# Duration of job for each position
jobs_durations = KIntVarArray()
# Completion time for each position
jobs_completions = KIntVarArray()
# Release date of job for each postion
jobs_release_dates = KIntVarArray()
### Creation of the problem
# Creation of the Kalis session
session = KSession()
# Creation of the optimization problem
problem = KProblem(session, "B-4 Sequencing")
# Compute some statistics
min_duration = min(durations)
max_duration = max(durations)
min_release_date = min(release_dates)
max_realease_date = max(release_dates)
min_due_date = min(due_dates)
max_due_date = max(due_dates)
max_time = max_realease_date + sum(durations)
for task_index in range(nb_tasks):
rank += KIntVar(problem, "rank(%d)" % task_index, 0, nb_tasks - 1)
jobs_start += KIntVar(problem, "start(%d)" % task_index, 0, max_time)
jobs_durations += KIntVar(problem, "dur(%d)" % task_index, min_duration, max_duration)
jobs_completions += KIntVar(problem, "comp(%d)" % task_index, 0, max_time)
jobs_release_dates += KIntVar(problem, "rel(%d)" % task_index, min_release_date, max_realease_date)
### Creation of the constraints
# One position per job
problem.post(KAllDifferent("alldiff(rank)", rank))
# Convert python lists data to KIntArray
K_durations = KIntArray()
K_release_dates = KIntArray()
for task_index in range(nb_tasks):
res = K_durations.add(durations[task_index])
res = K_release_dates.add(release_dates[task_index])
# Corresponding durations and jobs durations variables with a KElement constraint
# i.e. "durations[rank[task_index]] == jobs_durations[task_index]"
for task_index in range(nb_tasks):
duration_kelt = KEltTerm(K_durations, rank[task_index])
problem.post(duration_kelt == jobs_durations[task_index])
release_date_kelt = KEltTerm(K_release_dates, rank[task_index])
problem.post(release_date_kelt == jobs_release_dates[task_index])
# Ordering of starting dates between jobs
for task_index in range(nb_tasks - 1):
problem.post(jobs_start[task_index + 1] >= jobs_start[task_index] + jobs_durations[task_index])
# Ordering start times and release dates
for task_index in range(nb_tasks):
problem.post(jobs_start[task_index] >= jobs_release_dates[task_index])
# Job completion date is equal to its start date plus its duration
for task_index in range(nb_tasks):
problem.post(jobs_completions[task_index] == jobs_start[task_index] + jobs_durations[task_index])
# First propagation of the problem
if problem.propagate():
print("Problem is infeasible")
sys.exit(1)
### Solve the problem
# Set the branching scheme
my_branching_array = KBranchingSchemeArray()
my_branching_array += KSplitDomain(KSmallestDomain(), KMinToMax())
# Creation of the solver
solver = KSolver(problem, my_branching_array)
### Objective 1 : minimize the makespan
problem.setObjective(jobs_completions[nb_tasks - 1])
problem.setSense(KProblem.Minimize)
# Look for all feasible solutions
result = solver.optimize()
# Printing the solution
def printSequencingSolution(solution):
print("Completion time: ", solution.getObjectiveValue())
print("Release dates: ", end='\t')
for task_index in range(nb_tasks):
print(release_dates[task_index], end="\t")
print("\nDurations: ", end='\t')
for task_index in range(nb_tasks):
print(durations[task_index], end="\t")
print("\nStart dates: ", end='\t')
for task_index in range(nb_tasks):
print(solution.getValue(jobs_start[task_index]), end="\t")
print("\nEnd dates: ", end='\t')
for task_index in range(nb_tasks):
print(solution.getValue(jobs_completions[task_index]), end="\t")
print("\nDue dates: ", end='\t')
for task_index in range(nb_tasks):
print(due_dates[task_index], end="\t")
print("")
if result:
solution = problem.getSolution()
solution.printResume()
printSequencingSolution(solution)
### Objective 2: minimize the average completion time
jobs_completions_sum = 0
for task_index in range(nb_tasks):
jobs_completions_sum += jobs_completions[task_index]
# The average completion time is defined as equal to the sum of the completion times since it
# is equivalent for the optimization phase.
average_completion = KIntVar(problem, "average completion", 0, 1000)
problem.post(average_completion == jobs_completions_sum)
problem.setObjective(average_completion)
result = solver.optimize()
if result:
solution = problem.getSolution()
solution.printResume()
printSequencingSolution(solution)
### Objective 3: minimize the average completion time
# Declare lateness of each job as a variable
jobs_lateness = KIntVarArray()
for task_index in range(nb_tasks):
jobs_lateness += KIntVar(problem, "late(%d)" % task_index, 0, max_time)
# Declare due date of each job as a variable
jobs_due_dates = KIntVarArray()
for task_index in range(nb_tasks):
jobs_due_dates += KIntVar(problem, "due(%d)" % task_index, min_due_date, max_due_date)
# Convert python lists to KIntArray
K_due_dates = KIntArray()
for task_index in range(nb_tasks):
res = K_due_dates.add(due_dates[task_index])
# Set due date for each job (i.e. "jobs_due_dates[rank[task_index]] == due_dates[task_index]")
for task_index in range(nb_tasks):
due_date_kelt = KEltTerm(K_due_dates, rank[task_index])
problem.post(due_date_kelt == jobs_due_dates[task_index])
# Adding lateness constraint
lateness_sum = 0
for task_index in range(nb_tasks):
problem.post(jobs_lateness[task_index] >= jobs_completions[task_index] - jobs_due_dates[task_index])
lateness_sum += jobs_lateness[task_index]
total_lateness = KIntVar(problem, "total lateness", 0, nb_tasks * max_time)
problem.post(total_lateness == lateness_sum)
problem.setObjective(total_lateness)
result = solver.optimize()
if result:
solution = problem.getSolution()
print("Completion time: %d" % solution.getValue(jobs_completions[nb_tasks-1]))
print("average: %f" % (solution.getValue(average_completion) / nb_tasks))
print("Tardiness: %d" % solution.getValue(total_lateness))
printSequencingSolution(solution)
// Number of tasks
int NTASKS = 7;
// Release date of tasks
int REL[] = { 2, 5, 4, 0, 0, 8, 9};
// Duration of tasks
int DUR[] = { 5, 6, 8, 4, 2, 4, 2};
// Due date of tasks
int DUE[] = {10, 21, 15, 10, 5, 15, 22};
System.loadLibrary("KalisJava");
try
{
// Number of job at position k
KIntVarArray rank = new KIntVarArray();
// Start time of job at position k
KIntVarArray start = new KIntVarArray();
// Duration of job at position k
KIntVarArray dur = new KIntVarArray();
// Completion time of job at position k
KIntVarArray comp = new KIntVarArray();
// Release date of job at position k
KIntVarArray rel = new KIntVarArray();
KSession session = new KSession();
// Creation of the problem in this session
KProblem problem = new KProblem(session, "B-4 Sequencing");
// compute some statistics
int indexTask;
int MAXTIME = 0;
int MINDUR = Integer.MAX_VALUE;
int MAXDUR = 0;
int MINREL = Integer.MAX_VALUE;
int MAXREL = 0;
int MINDUE = Integer.MAX_VALUE;
int MAXDUE = 0;
int SDUR = 0;
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
if (MINDUR > DUR[indexTask])
{
MINDUR = DUR[indexTask];
}
if (MAXDUR < DUR[indexTask])
{
MAXDUR = DUR[indexTask];
}
if (MINREL > REL[indexTask])
{
MINREL = REL[indexTask];
}
if (MAXREL < REL[indexTask])
{
MAXREL = REL[indexTask];
}
if (MINDUE > DUE[indexTask])
{
MINDUE = DUE[indexTask];
}
if (MAXDUE < DUE[indexTask])
{
MAXDUE = DUE[indexTask];
}
SDUR += DUR[indexTask];
}
MAXTIME = MAXREL + SDUR;
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
rank.add(new KIntVar(problem, "use(" + indexTask + ")", 0, NTASKS - 1));
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
start.add(new KIntVar(problem, "start(" + indexTask + ")", 0, MAXTIME));
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
dur.add(new KIntVar(problem, "dur(" + indexTask + ")", MINDUR, MAXDUR));
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
comp.add(new KIntVar(problem, "comp(" + indexTask + ")", 0, MAXTIME));
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
rel.add(new KIntVar(problem, "rel(" + indexTask + ")", MINREL, MAXREL));
}
// One position per job
problem.post(new KAllDifferent("alldiff(rank)", rank));
// Duration of job at position k
KIntArray idur = new KIntArray();
KIntArray irel = new KIntArray();
KIntArray idue = new KIntArray();
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
idur.add(DUR[indexTask]);
irel.add(REL[indexTask]);
idue.add(DUE[indexTask]);
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
KEltTerm kelt = new KEltTerm(idur, rank.getElt(indexTask));
problem.post(new KElement(kelt, dur.getElt(indexTask)));
// Release date of job at position k
KEltTerm keltrel = new KEltTerm(irel, rank.getElt(indexTask));
problem.post(new KElement(keltrel, rel.getElt(indexTask)));
}
for (indexTask = 0; indexTask < NTASKS - 1; indexTask++)
{
// Sequence of jobs
// Create the linear combination start.getElt(indexTask+1) - start.getElt(indexTask) - dur.getElt(indexTask))
KLinTerm linearTerm = new KLinTerm();
linearTerm.add(start.getElt(indexTask+1),1);
linearTerm.add(start.getElt(indexTask),-1);
linearTerm.add(dur.getElt(indexTask),-1);
// add the linear combination equality startDates[3] - 1 * startDates[0] - varObj == 0
KNumVarArray intVarArrayToSet = linearTerm.getLvars();
KDoubleArray coeffsToSet = linearTerm.getCoeffs();
problem.post(new KNumLinComb("",coeffsToSet,intVarArrayToSet,0,KNumLinComb.LinCombOperator.GreaterOrEqual));
}
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
// Start times
problem.post(new KGreaterOrEqualXyc(start.getElt(indexTask), rel.getElt(indexTask), 0));
// Completion times
// Create the linear combination comp.getElt(indexTask) - start.getElt(indexTask) - dur.getElt(indexTask)
KLinTerm linearTerm = new KLinTerm();
linearTerm.add(comp.getElt(indexTask),1);
linearTerm.add(start.getElt(indexTask),-1);
linearTerm.add(dur.getElt(indexTask),-1);
// add the linear combination equality startDates[3] - 1 * startDates[0] - varObj == 0
KNumVarArray intVarArrayToSet = linearTerm.getLvars();
KDoubleArray coeffsToSet = linearTerm.getCoeffs();
problem.post(new KNumLinComb("",coeffsToSet,intVarArrayToSet,0,KNumLinComb.LinCombOperator.Equal));
}
// propagating problem
if (problem.propagate())
{
System.out.println("Problem is infeasible");
exit(1);
}
// Set the branching strategy
KBranchingSchemeArray myBa = new KBranchingSchemeArray();
myBa.add(new KSplitDomain(new KSmallestDomain(), new KMinToMax()));
// creation of the solver
KSolver solver = new KSolver(problem, myBa);
// **********************
// Objective 1: Makespan
// **********************
problem.setObjective(comp.getElt(NTASKS - 1));
problem.setSense(KProblem.Sense.Minimize);
// look for all solutions
int result = solver.optimize();
// solution printing
KSolution sol = problem.getSolution();
// print solution resume
sol.printResume();
// solution printing
System.out.println("Completion time: " + problem.getSolution().getValue(comp.getElt(NTASKS - 1)));
System.out.print("Rel\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(REL[indexTask] + "\t");
}
System.out.print("\nDur\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUR[indexTask] + "\t");
}
System.out.print("\nStart\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(start.getElt(indexTask)) + "\t");
}
System.out.print("\nEnd\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(comp.getElt(indexTask)) + "\t");
}
System.out.print("\nDue\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUE[indexTask] + "\t");
}
System.out.print("\n");
// ***************************************
// Objective 2: Average completion time:
// ***************************************
KLinTerm totalCompletionTerm = new KLinTerm();
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
totalCompletionTerm.add(comp.getElt(indexTask), 1);
}
KIntVar averageCompletion = new KIntVar(problem, "average completion", 0, 1000);
// Create the linear combination averageCompletion - totalCompletionTerm
totalCompletionTerm.add(averageCompletion,-1);
KNumVarArray intVarArrayToSet = totalCompletionTerm.getLvars();
KDoubleArray coeffsToSet = totalCompletionTerm.getCoeffs();
problem.post(new KNumLinComb("",coeffsToSet,intVarArrayToSet,0,KNumLinComb.LinCombOperator.Equal));
problem.setObjective(averageCompletion);
result = solver.optimize();
// solution printing
System.out.println("Completion time: " + problem.getSolution().getValue(comp.getElt(NTASKS - 1)));
System.out.println("average: " + problem.getSolution().getValue(averageCompletion));
System.out.print("\nRel\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(REL[indexTask] + "\t");
}
System.out.print("\nDur\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUR[indexTask] + "\t");
}
System.out.print("\nStart\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(start.getElt(indexTask)) + "\t");
}
System.out.print("\nEnd\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(comp.getElt(indexTask)) + "\t");
}
System.out.print("\nDue\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUE[indexTask] + "\t");
}
System.out.print("\n");
// *****************************
// Objective 3: total lateness:
// *****************************
// Lateness of job at position k
KIntVarArray late = new KIntVarArray();
// Due date of job at position k
KIntVarArray due = new KIntVarArray();
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
due.add(new KIntVar(problem, "due(" + indexTask + ")", MINDUE, MAXDUE));
late.add(new KIntVar(problem, "late(" + indexTask + ")", 0, MAXTIME));
}
// Due date of job at position k
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
KEltTerm keltdue = new KEltTerm(idue, rank.getElt(indexTask));
problem.post(new KElement(keltdue, due.getElt(indexTask)));
}
KLinTerm totLatTerm = new KLinTerm();
// building each tasks with fixed time horizon (0..HORIZON)
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
// Late jobs: completion time exceeds the due date
// Create the linear combination late.getElt(indexTask) - comp.getElt(indexTask) + due.getElt(indexTask)
KLinTerm linearTerm = new KLinTerm();
linearTerm.add(late.getElt(indexTask),1);
linearTerm.add(comp.getElt(indexTask),-1);
linearTerm.add(due.getElt(indexTask),+1);
// add the linear combination equality startDates[3] - 1 * startDates[0] - varObj == 0
KNumVarArray intVarArrayToSet_linearTerm = linearTerm.getLvars();
KDoubleArray coeffsToSet_linearTerm = linearTerm.getCoeffs();
problem.post(new KNumLinComb("",coeffsToSet_linearTerm,intVarArrayToSet_linearTerm,0,KNumLinComb.LinCombOperator.GreaterOrEqual));
totLatTerm.add(late.getElt(indexTask), 1);
}
KIntVar totLate = new KIntVar(problem, "total lateness", 0, 1000);
totLatTerm.add(totLate,-1);
// add the linear combination equality startDates[3] - 1 * startDates[0] - varObj == 0
KNumVarArray intVarArrayToSet_totLatTerm = totLatTerm.getLvars();
KDoubleArray coeffsToSet_totLatTerm = totLatTerm.getCoeffs();
problem.post(new KNumLinComb("",coeffsToSet_totLatTerm,intVarArrayToSet_totLatTerm,0,KNumLinComb.LinCombOperator.Equal));
problem.setObjective(totLate);
result = solver.optimize();
// solution printing
System.out.println("Completion time: " + problem.getSolution().getValue(comp.getElt(NTASKS - 1)));
System.out.println("average: " + problem.getSolution().getValue(averageCompletion));
System.out.println("Tardiness: " + problem.getSolution().getValue(totLate));
System.out.print("\nRel\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(REL[indexTask] + "\t");
}
System.out.print("\nDur\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUR[indexTask] + "\t");
}
System.out.print("\nStart\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(start.getElt(indexTask)) + "\t");
}
System.out.print("\nEnd\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(comp.getElt(indexTask)) + "\t");
}
System.out.print("\nDue\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(DUE[indexTask] + "\t");
}
System.out.print("\nLate\t");
for (indexTask = 0; indexTask < NTASKS; indexTask++)
{
System.out.print(problem.getSolution().getValue(late.getElt(indexTask)) + "\t");
}
System.out.print("\n");
}
catch (Exception e)
{
e.printStackTrace();
}
Results¶
The minimum makespan of the schedule is 31, the minimum sum of completion times is 103 (which gives an average of 103 / 7 = 14. 71). A schedule with this objective value is 5  4
4  1
1  6
6  2
2  3. If we compare the completion times with the due dates we see that jobs 1, 2, 3, and 6 finish late (with a total tardiness of 21). The minimum tardiness is 18. A schedule with this tardiness is 5
3. If we compare the completion times with the due dates we see that jobs 1, 2, 3, and 6 finish late (with a total tardiness of 21). The minimum tardiness is 18. A schedule with this tardiness is 5  1
1  4
4  6
6  2
2  7
7  3 where jobs 4 and 7 finish one time unit late and job 3 is late by 16 time units, and it terminates at time 31 instead of being ready at its due date, time 15. This schedule has an average completion time of 15.71.
3 where jobs 4 and 7 finish one time unit late and job 3 is late by 16 time units, and it terminates at time 31 instead of being ready at its due date, time 15. This schedule has an average completion time of 15.71.