Controlling the solution search

In this chapter, you will be introduced to search control. It includes:

• a short description of the main principles ;

• a presentation of the default strategy for optimization ;

• the objects involved in search control.

Method description

Search is made thanks to a tree search algorithm. At each node, propagation is made and if no solution exists, Artelys Kalis needs to split your problem in smaller subproblems covering (or not) all the initial problem. This partition is made following a branching scheme. Here is a figure (Fig. 6) explaining that:

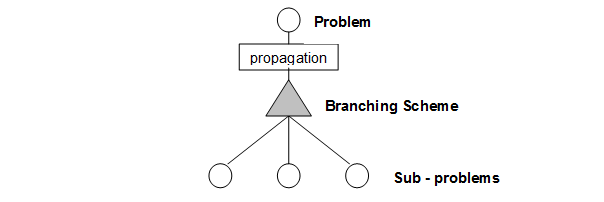
Fig. 6 Tree search algorithm

Different types of branching schemes exist. For example, a classical way is to choose a variable which has not been instantiated so far and to build a sub-problem for each remaining value in the variable’s domain, this sub-problem being the original problem where propagation the variable has been instantiated to this value. And then, you can continue the search with these new nodes.

Choosing the right branching schemes to be used with your particular problem could greatly improve the performance of the tree search. Artelys Kalis allows you to choose between many classical branching schemes provided with the library and to easily program yourself the more specialized branching schemes that you suppose to be useful with your own problems.

Here are classical branching schemes available in Artelys Kalis:

Fig. 7 Classical branching schemes

KAssignVar

As explained above, it chooses a variable X and creates one sub-problem for each possible value of X.

KAssignAndForbid

In this case, it chooses a variable X and creates one node where X is equal to v (a value currently in X’s domain) and another node where X must be different from v.

KSplitDomain

This branching scheme is mainly used in mixed-integer linear programming. It chooses a variable X and creates one node where X is lower or equal to a value v (not necessary in X’s domain but it must be between its lower and upper bound) and a second node where X is greater than v.

KSettleDisjunction

It is the only branching scheme not working on variables. It works on binary disjunctions between constraints (for example “C1 or C2”). Then it creates two nodes splitting domain in different possibilities for the status of C1 and C2.

Note that these branching schemes explore the left branch before the right one.

These KBranchingScheme often need to select an unassigned variable and choose a value. These two principles give two objects in Artelys Kalis: a KVariableSelector and a KValueSelector. Some classes are inheriting from them in order to offer some usual behaviors but you may also add new ones easily.

Here are some examples of KVariableSelector:

• KSmallestDomain: looks for an unassigned variable having the smallest number of values in its domain.

• KSmallestMin: looks for an unassigned variable having the smallest lower bound.

• KMaxDegree: the degree is the static number of constraints in which a variable is involved. This selector looks for an unassigned variable having the biggest degree.

and some examples of KValueSelector:

• KMinToMax: returns the lower bound of a variable. It helps choosing variables in increasing order.

• KNearestValue: returns the value currently in domain which is the nearest of a specific target value. It is useful for heuristics trying to be close to a wished solution.

The complete list is available in the Artelys Kalis Reference Manual.

In fact, when branching, you can distinguish 3 different objects:

• branching scheme: it explains how to create new nodes.

• branching object: the object which is involved in this branching: it can be a variable, a constraint (as seen before) but it could also be any type of object.

• branching information: it represents the information that must be kept while you are creating each node (it can be the last value which was given to a variable (the branching object)).

Artelys Kalis is based on these three concepts in order to help you creating many branching schemes. We will see how to do so in the following sections.

Controlling strategies used by a KSolver

Now that you have a better understanding ot the branching scheme, let’s us introduce them in our search. The control of the solution search is performed by telling the KSolver object how it must branch during all the tree search.

The branching schemes are represented by KBranchingScheme objects stored by the KSolver object used to solve the problem. These objects can be gathered to a KBranchingSchemeArray object. This object represents an ordered set of KBranchingScheme objects and can be declared this way:

C++PythonJava

KBranchingSchemeArray myBranchingArray;

For example, we can put into myBranchingArray an object of the KAssignVar class: this class is a subclass of KBranchingScheme provided with Artelys Kalis. Here is how it can be done:

C++PythonJava

myBranchingArray += KAssignVar();

Here we have built a KAssignVar object using the default constructor and put it in myBranchingArray using the overloaded operator+=. Assuming that we have already declared a KProblem object myProblem, the code declaring the solver which will use our KAssignVar branching scheme:

C++PythonJava

KSolver mySolver(myProblem, myBranchingArray);

Here we have used a new constructor of the KSolver class, which takes a KBranchingSchemeArray parameter in addition to the first KProblem parameter.

If your array contains more than one branching schemes, the solver will use them in the same order as in the KBranchingSchemeArray. It means that at each node, the KSolver will try to branch thanks to the first branching scheme and if it is not possible, he will try with the second one and the third one, … until it is able to make new branches. For example, you may start with KAssignVar working on a small list of variables at first and then KAssignVar on all other variables. This could be done by creating two KAssignVar objects, each of them with their specific list of variables as argument, and adding them to the KBranchingSchemeArray given to the KSolver. It is really useful when your problem is bilevel: investment and scheduling, rest or type of work, …

Here is the code:

C++PythonJava

KIntVarArray mainVar(myProblem, nbMainVar, 0, 1, "MainVar");
KIntVarArray otherVar(myProblem, nbOtherVar, 0, 10, "OtherVar");

KBranchingSchemeArray branchingArr;

branchingArr += KAssignVar(KSmallestDomain(), KMinToMax(), mainVar);
branchingArr += KAssignVar(KSmallestDomain(), KMinToMax(), otherVar);

KSolver mySolver(myProblem, branchingArr);

Here you can also see that KAssignVar has different constructors and that one of them is using a KVariableSelector, a KValueSelector and a list of variables.

The default strategy

In order to prevent Artelys Kalis to stop in a non-final state at one node (it means that some variables are not instantiated) for which current branching schemes given to the solver cannot provide new branching objects (in fact new nodes), or the user to specify branching schemes to be used, a default branching scheme will always be applied after the one given to the KSolver. This is a KAssignVar: in the particular context of the default scheme, it will choose among all the variables the one with the smallest domain and assign it the Largest possible value first.

Note

For some branching schemes, there is always at least one branching object to work on. That is for example the case with a KAssignVar working with all variables: either a given node is a solution of the problem and no more branching has to be performed, or there is at least one non instantiated variable. In the latter case, the KAssignVar can choose the non instantiated variable to build new nodes. The outcome of this is that if you put a branching scheme like a KAssignVar working with all variables at the top of your branching schemes array, the other branching schemes will never be used.