Artelys Knitro 11.1 : Résolution ultra-rapide des problèmes sans dérivées !
Cas d’application : Découvrez comment nos clients approximent leurs dérivées en macroéconomie !
La macroéconomie inclut notamment l’étude de modèles nommés DGSE (pour modèles d’Equilibre Général Dynamique Stochastique) qui visent à représenter les effets des politiques économiques sur la croissance d’un pays. Ces modèles sont fréquemment utilisés par les banques centrales pour estimer la croissance nationale globale.
Nous avons travaillé sur les modèles DGSE de la Federal Reserve Bank of New York, implémentés en Matlab avec la toolbox IRIS par Iskander Karibzhanov, économiste pour la Banque du Canada. Ce modèle est un modèle fortement non linéaire pour lequel les dérivées exactes ne peuvent être fournies. Dans ce cas, le solveur approxime les dérivées par différences finies mais il n’est pas possible de les évaluer avec autant de précision que lorsque les dérivées exactes sont fournies.
La parallélisation des différences finies avec Artelys Knitro permet d’accélérer la résolution. L’utilisation de Knitro 11.1 a permis de réduire le temps de calcul d’un facteur 5 sur les instances étudiées tout en maintenant la qualité de la solution obtenue !

Nouvelle option de warm-start pour les méthodes de points intérieurs
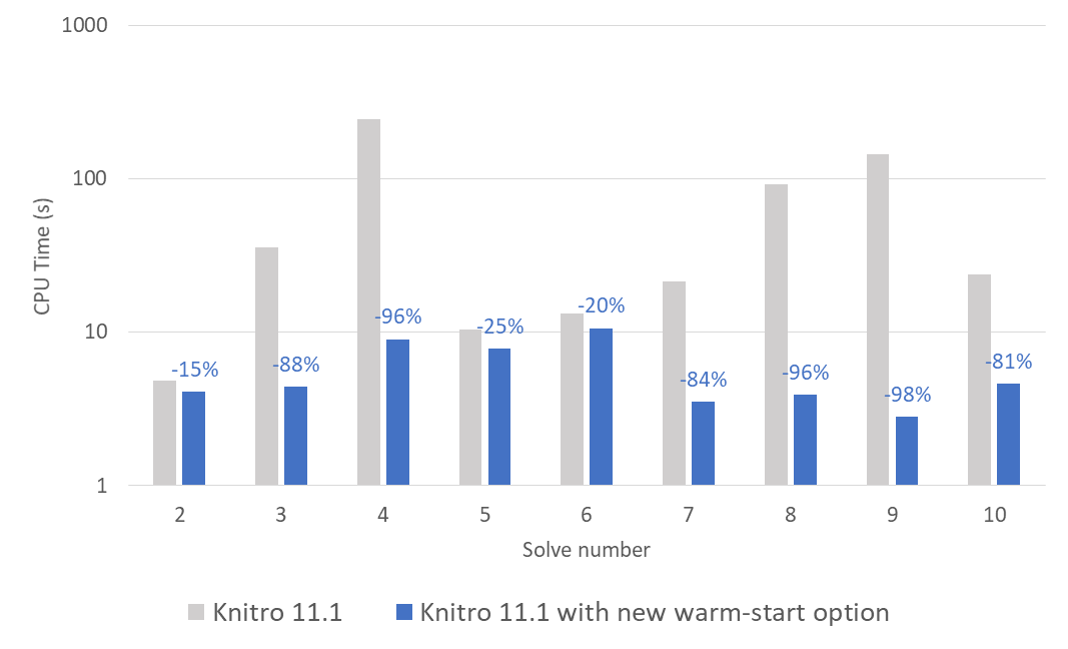
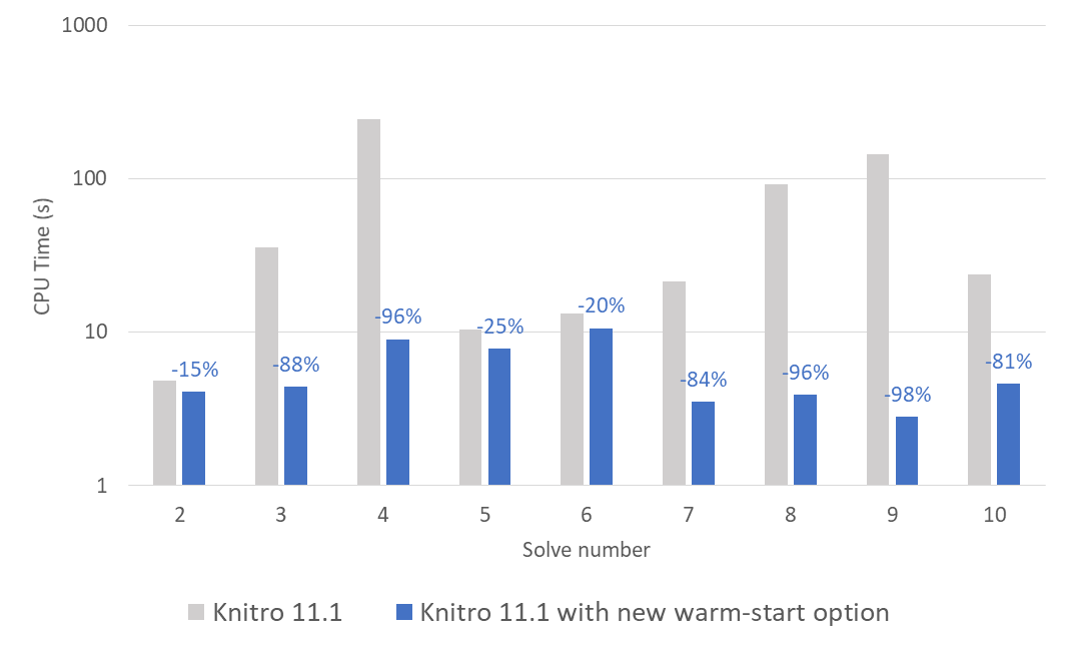
Cette version voit également l’apparition d’une nouvelle option dédiée au warm-start pour les méthodes de points intérieurs (algorithmes 1&2). L’activation de cette option permet une résolution ultra-rapide de vos problèmes lorsque l’utilisateur a la connaissance d’un bon point initial. Cette option est particulièrement efficace pour les modèles nécessitant la résolution séquentielle de problèmes non linéaires. La figure ci-dessous présente un cas d’application nécessitant la résolution séquentielle de sous-problèmes non linéaires pour laquelle l’activation de l’option de warm-start divise le temps de calcul total par 10 !
Autres fonctionnalités d’Artelys Knitro 11.1
• Nouvelle API Python permettant une déclaration fine de la structure des contraintes (eg linéaire, quadratique, conique)
• Détection automatique de la convexité des problèmes QP/QCQP
• Nouvelles coupes de sac à dos liftées dédiées aux problèmes MINLP
• Amélioration de l’approximation L-BFGS
• Augmentation générale des performances sur les problèmes convexes en particulier pour les instances de très grande taille

Améliorer la planification de production des transformateurs électriques grâce à des solutions d’intelligence artificielle
Améliorer la planification de production de transformateurs haute tension à l’usine Hitachi Energy de Varennes grâce à des solutions avancées d’intelligence artificielle.

Artelys accompagne la Commission de Régulation de l’Énergie (CRE) dans l’évaluation des niveaux d’incitation adéquats pour favoriser la performance des réseaux de distribution dans le cadre du TURPE 7
Artelys a réalisé une étude quantitative pour informer les propositions de niveaux cibles pour le TURPE 7, en analysant les résultats historiques et l’impact de l’intégration des données des compteurs communicants (Linky) dans les indicateurs mesurant la qualité de l’alimentation.

Le projet MARI s’élargit
Ces derniers mois, plusieurs nouveaux GRT européens ont rejoint avec succès MARI, la plateforme paneuropéenne d’activation de la réserve de remplacement (mFRR), dont l’algorithme d’enchère a été développé par Artelys.

Knitro 14.2 résout vos modèles non-convexes difficiles en un instant
– Nous avons le plaisir d’annoncer qu’Artelys Knitro 14.0 est maintenant disponible ! Cette nouvelle version permet aux entreprises de résoudre des problèmes complexes d’optimisation non linéaire avec une efficacité et une précision sans précédent.